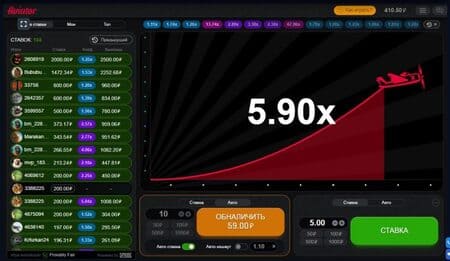
На данный момент в онлайн казино есть две версии краш эмулятора Aviator. Обновление появилось в 2021 году и получило более современный дизайн. Теперь все основывается на генераторе случайных чисел. Что касается механики, то она не изменилась.
Правила игры Aviator
Готовимся к старту
Выбираем размер ставки перед полетом. Вы увидите крутящийся пропеллер и надпись «Ожидаем новый раунд», за это время, которое составляет примерно 5 секунд, нужно выбрать в панели управления размер ставки перед полетом. Можно ввести значение с клавиатуры или благодаря быстрым кнопкам, ограничение максимальной ставки – 100.

Панель управления
Она располагается снизу радара с двумя отдельными зелеными кнопками «Ставка». Вы можете зарегистрировать сразу две параллельных бета. В таком случае важно успевать обналичивать нужный коэффициент. Для удобства набора есть фиксированные беты и режим авто игры.
Старт полета
Сумма поставлена самолетик взлетает и показывается на радаре. Пройденный путь отмечается красной линией, воздушное судно постепенно продвигается в правую часть экрана.

Набор высоты
На экране мы видим нарастающий множитель. Нужно быть предельно внимательным, так как в определенный момент кукурузник может покинуть зону радара.

Умножение ставки
Ваш выигрыш может быть рассчитан в любой момент, на том множителе, на котором вы хотите остановиться, до тех пор пока самолет не улетел.
После запуска краш игры Авиатор пользователю предстоит выполнять самые разные задания:
- Наблюдать, как летит воздушное судно
- Игрок будет не свидетелем полета самолета, а будет иметь возможность принимать решения.
- В процессе игры самолет пролетает в рамках радара и отмечается красным логотипом.
- Во время полета стремительно растет множитель, который будет применяться к основной ставке. Гемблер может получить выплату от х1 до х1000.
Видео обзор как играть в авиатор

Важно отметить и тот факт, что ставка перемножается на тот множитель, на котором была оставлена игра. Если игрок не смог словить коэффициент и закрыть ставку до момента исчезновения кукурузника, то раунд будет проигранным. Ваша ставка сгорает.
Раунды запускаются в автоматическом режиме. Между турами перерыв всего в 5 секунд. Пользователи имеют возможность спокойно пропускать определенные полеты, при этом, не теряя собственных средств.
Провайдер и лицензии слота Авиатор
Производителем софта выступает бренд Spribe. Это компания из Грузии, которая специализируется на разработке слотов. Несколько лет назад компания решила рискнуть и представить общественности кардинально новый слот. И всего за полгода данная игра стала одной из самых популярных и востребованных в игровой индустрии гемблинга.

Разработчик Spribe имеет множество лицензий в разных юрисдикциях, подробнее вы можете посмотреть на официальном сайте провайдера.

Функционал слота
Разработчики игры Авиатор включили в игровой процесс 3 полезные функции. Многие начинающие игроки просто не обращают на них никакого внимания и упускают тем самым свою выгоду.
Автоматическая игра
Благодаря этой опции гемблер имеет возможность определить коэффициент на котором он остановится и зафиксировать свою ставку на каждый раунд. К примеру, игрок хочет закрыть пари при множителе в х50. Это говорит о том, что когда самолет доберется до данной отметки, то слот автоматически рассчитывает выплату. Задача игрока состоит в том, что бы дождаться, когда самолет все-таки преодолеет нужную высоту.
Особенность фиксации ставки очень удобна при долгосрочной дистанции на эмуляторе. Многие игроки делают расчет в слоте именно на большие множители. Самолет может добраться до самых разных отметок, даже в х1000. Однако лучше всего придерживаться золотой середины при авто игре и сильно не задирать планку, ведь даже х50 может принести хорошую выплату.
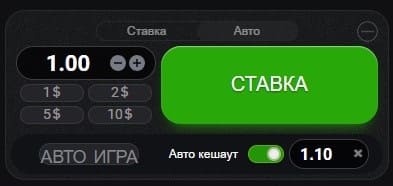
Чтобы активировать функцию нужно лишь переместить ползунок в режим авто и зафиксировать ставку «Авто кешаут» как это показано на картинке:
Статистика
Всегда нужно анализировать игровой процесс и понимать, что ГСЧ выдает огромное множество вариации. Статистка говорит о том, что множитель в х100 будет появляться раз в 1-2 часа. Понимая такой расклад, пользователь получает возможность разработать собственную стратегию. И если уже прошел час, то можно рискнуть и поставить больше. По факту комбинаций и вариантов великое множество, и все они всегда отображаются в статистике в верхней вкладке «История раундов».

Демо вариант
Важно отметить, что играть в данный слот можно играть абсолютно бесплатно, без вложений личных средств. Это плюс для той категории пользователей, которые не имеют опыта. То есть можно потренироваться и привыкнуть к игре, понять, как устроен слот, и уже после этого переходить к реальным ставкам. Но для этого потребуется пройти регистрацию на сайте онлайн казино Пин-ап. После внесения депозита на личный счет можно смело запускать Авиатор и начинать полет. Понять что вы играете в режиме демо можно по желтой вкладке «Fun mode».

Ставки Aviator
Ниже основной панели краш эмулятора расположены ставки. Но перед тем как их делать, геймеру нужно внести на счет средства. И для этого есть несколько проверенных методов:
- Банковские карты.
- Онлайн кошельки.
- Альтернативные агрегаторы для переводов.
- Крипто-биржи.
Максимальная ставка 100$. Клик по быстрой ставке увеличивает ее размер на соответствующий номинал. С размерами бетов нужно определиться до начала следующего полета. Времени на это дается всего 5 секунд, так что нужно быть внимательным.
Важно: вы можете поставить сразу две параллельных ставки по которым будут рассчитываться выигрыши.
После взлета самолета игрок имеет возможность в любой момент получить выплату по текущему коэффициенту. И его можно фиксировать (как опция авто игры, описанная выше).
Приложение Aviator довольно удобное, тем более не имеет никаких закладок или настроек, на главном экране только то, что действительно нужно и важно.
Разумеется, игрок самостоятельно определяет для себя размер ставки. Но вначале лучше сильно не рисковать и устанавливать одну ставку на минимальные значения.
Стратегии игры
Тут начинающему гемблеру будет непросто. Но если подходить к игровому процессу с трезвой головой, анализировать все и правильно оценивать возможности, то количество побед и сумма выигрышей будет больше, чем количество поражений. Минимизировать риски можно по-разному. Обсудим основные стратегии, которые приемлемы для слота Авиатор.
Бюджетная система
Перед началом игрового процесса нужно определить для себя оптимальный размер ставки и предел автоматического кэшаута.

Не забываете так же следить за статистикой если до этого были большие коэффициенты, то лучше еще подождать. Делаем беты на ваш профит и стараемся брать высокие множители.
Похожая стратегия используется в подсчете блекджека.
Это тактика уже проверенная многими игроками, она не требует серьезных вложений. Но нужно отметить, что депозита в 100 рублей вряд ли будет достаточно для получения выигрыша в долгосрочной перспективе. Занести сразу лучше несколько тысяч, и после использовать все возможности бонусной программы для зарегистрированных пользователей.
Мартингейл
Это универсальный метод, который используют как беттеры, так и гемблеры. И игра не имеет никакого значения, важно лишь ограничение размера ставок.

Ответы по популярные вопросы

